Your favorite equation

it can be anything math, physics, a joke like the one where girls = evil and the proof for it.

my is e^ix= cos x + i sin x 

I could prove that 0=1 ^ 0=2

It would take a while do do it on a forum though...I might scan it  

I could prove that 0=1 ^ 0=2

 

It would take a while do do it on a forum though...I might scan it

a55assin

I could prove that 0=1 ^ 0=2

It would take a while do do it on a forum though...I might scan it

a55assin

[QUOTE="a55assin"]

I could prove that 0=1 ^ 0=2

 

It would take a while do do it on a forum though...I might scan it

Robograndma

Totally different...I could prove it with an equation...try proving that 0=2...c'mon. 

.....Omni-Slash

it can be anything math, physics, a joke like the one where girls = evil and the proof for it.

my is e^ix= cos x + i sin x 

Chessy_Nachos

[QUOTE="a55assin"]

I could prove that 0=1 ^ 0=2

 

It would take a while do do it on a forum though...I might scan it

Robograndma

I hate math...Canuck3000

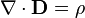
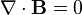
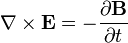
Given that a and b are integers such that a = b, Prove: 0 = 2

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. a(a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

oh ya..and every of those (a2) and (b2) is actually squared...becuase Im too lazy using the symbol

I could prove that 0=1 ^ 0=2

 

It would take a while do do it on a forum though...I might scan it

a55assin

Given that a and b are integers such that a = b, Prove: 0 = 2

 

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. (a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

 

oh ya..and every of those (a2) and (b2) is actually squared...becuase Im too lazy using the symbol

a55assin

 

Given that a and b are integers such that a = b, Prove: 0 = 2

 

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. (a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

a55assin

[QUOTE="a55assin"]

Given that a and b are integers such that a = b, Prove: 0 = 2

 

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. (a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

 

oh ya..and every of those (a2) and (b2) is actually squared...becuase Im too lazy using the symbol

Chessy_Nachos

If you can understand it...it is. 

.....Omni-Slash

[QUOTE="a55assin"]

I could prove that 0=1 ^ 0=2

 

It would take a while do do it on a forum though...I might scan it

Chessy_Nachos

[QUOTE="a55assin"]

Given that a and b are integers such that a = b, Prove: 0 = 2

 

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. (a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

xaos

Step 7 and 8 consist of the Distributive property.

[QUOTE="xaos"][QUOTE="a55assin"]

Given that a and b are integers such that a = b, Prove: 0 = 2

 

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. (a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

a55assin

Step 7 and 8 consist of the Distributive property.

 He meant that step 8 should be:

 8. a(a - b) = (a - b)(b + 2)

thats how you got to

9. a = b + 2

by dividing both sides by (a-b).

the a was missing on the left side in 8. 

[QUOTE="xaos"][QUOTE="a55assin"]

Given that a and b are integers such that a = b, Prove: 0 = 2

 

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. (a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

a55assin

Step 7 and 8 consist of the Distributive property.

[QUOTE="a55assin"][QUOTE="xaos"][QUOTE="a55assin"]

Given that a and b are integers such that a = b, Prove: 0 = 2

 

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. (a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

Aznsilvrboy

Step 7 and 8 consist of the Distributive property.

He meant that step 8 should be:

8. a(a - b) = (a - b)(b + 2)

thats how you got to

9. a = b + 2

by dividing both sides by (a-b).

the a was missing on the left side in 8.

OH crap...I'm sorry, that was stupid of me. 

[QUOTE="a55assin"][QUOTE="xaos"][QUOTE="a55assin"]

Given that a and b are integers such that a = b, Prove: 0 = 2

 

1. a = b

2. a - b - 2 = a - b - 2

3. a(a - b - 2) = b(a - b - 2)

4. a2 - ab - 2a = ab - b2 - 2b

5. a2 - ab = ab - b2 - 2b + 2a

6. a2 - ab = ab + 2a - b2 - 2b

7. a(a - b) = a(b + 2) - b(b + 2)

8. (a - b) = (a - b)(b + 2)

9. a = b + 2

10. b = b + 2

11. Thereforem 0 = 2

xaos

Step 7 and 8 consist of the Distributive property.

Congrats...lol 

You people and your mathematics...

Don't any of you know of Godel's Incompleteness Theorem that proves that mathematics is an incomplete proof system?

You're all just wasting your time. :P 

sorry omni... step 1 is flawed... woman is time "and" money equates to woman = time+ money...

heres mine...

You people and your mathematics...

Don't any of you know of Godel's Incompleteness Theorem that proves that mathematics is an incomplete proof system?

You're all just wasting your time. :P 

The_Ish

You people and your mathematics...

Don't any of you know of Godel's Incompleteness Theorem that proves that mathematics is an incomplete proof system?

You're all just wasting your time. :P

The_Ish

[QUOTE="The_Ish"]

You people and your mathematics...

Don't any of you know of Godel's Incompleteness Theorem that proves that mathematics is an incomplete proof system?

You're all just wasting your time. :P

Chessy_Nachos

And heres one to go:

And heres one to go:

haloraider

[QUOTE="The_Ish"]

You people and your mathematics...

Don't any of you know of Godel's Incompleteness Theorem that proves that mathematics is an incomplete proof system?

You're all just wasting your time. :P

Chessy_Nachos

It's actually pretty famous (especially among Comp. Sci. majors):

http://www.mozilla.org/editor/midasdemo/securityprefs.html

The only problem you might find is that you might have to know some Discrete Mathematics beforehand. :?

.

It's basically the answer to perfection.

And heres one to go:

haloraider